MEMAHAMI ALGORITMA PENCARIAN DENGAN PENDEKATAN COMPUTATIONAL THINKING

Tujuan Pembelajaran
- Memahami konsep dasar algoritma pencarian biner.
- Mengimplementasikan pencarian biner dalam memecahkan persoalan pencarian.
Pencarian Biner (Binary Search) adalah metode pencarian yang bekerja dengan membagi data menjadi dua bagian, lalu membandingkan data pada salah satu bagian dengan target yang dicari. Proses ini memerlukan indeks terkecil dan terbesar untuk dihitung rata-rata, yang kemudian digunakan untuk menentukan bagian mana yang akan diperiksa lebih lanjut. Jika nilai yang dicari tidak ada dalam data, maka akan dikembalikan -1 atau indikasi bahwa nilai tidak ditemukan. Metode ini hanya dapat digunakan pada data yang telah diurutkan, dan secara signifikan lebih efisien dibandingkan dengan pencarian linear (linear search).

Dekomposisi membantu kita memecah pencarian biner menjadi langkah-langkah berikut:
- Urutkan data sebelum melakukan pencarian.
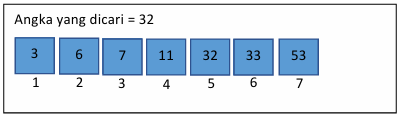
- Tentukan batas awal, tengah, dan akhir dari data.
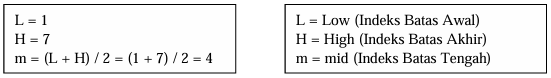
Catatan: Jika hasil perhitungan nilai mid berupa angka desimal (misalnya 0,5), bulatkan nilai indeks ke bawah.
- Bandingkan elemen tengah dengan elemen yang dicari.
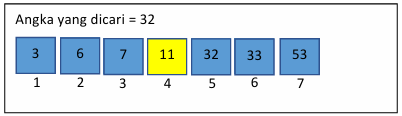
- Jika cocok, pencarian selesai.
- Jika elemen yang dicari lebih kecil dari elemen tengah, periksa setengah bagian kiri data.
- Jika elemen yang dicari lebih besar, periksa setengah bagian kanan data.
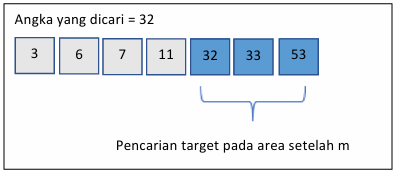
- Ulangi proses hingga elemen ditemukan atau ruang pencarian habis.
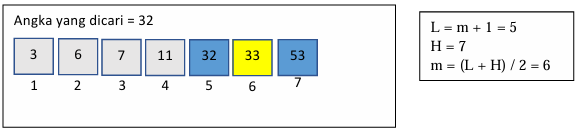
Berdasarkan rumus diatas, didapatkan nilai m atau mid = 6, yang berarti nilai tengahnya adalah angka yang ada pada indeks ke-6 yaitu 33. Mari kita periksa lagi apakah angka 33 sama dengan angka yang dicari? Jawabannya adalah tidak.
Lanjutkan pencarian.
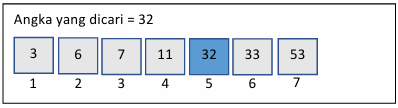
Pencarian target pada area sebelum m adalah indeks ke-5. Apakah nilai yang ada dalam indeks ke-5 sama dengan angka yang dicari? Jawabannya adalah YA, maka pencarian selesai.

Pola yang bisa dikenali dalam pencarian biner:
- Data harus terurut sebelum pencarian dilakukan.
- Setiap iterasi mengurangi ruang pencarian menjadi setengahnya, sehingga lebih cepat dibandingkan pencarian linear.

- Jika elemen berada di bagian awal atau akhir data, pencarian masih efisien karena tidak perlu memeriksa setiap elemen satu per satu.

Perhatikan barisan angka berikut. Untuk melihat visualisasi cara kerja algoritma pencarian biner, cobalah masukkan angka “17” sebagai target pada kolom masukan.

Dalam pencarian biner, kita dapat menyederhanakan masalah sebagai berikut:
- Bayangkan mencari nama dalam data siswa yang sudah diurutkan secara alfabetis.
- Dengan hanya membandingkan elemen tengah dan mempersempit ruang pencarian, kita tidak perlu mengecek semua elemen satu per satu.

Berikut adalah langkah-langkah algoritma pencarian biner:
- Pastikan data sudah terurut.
- Tentukan indeks awal (low), indeks akhir (high), dan indeks tengah (mid).
- Bandingkan elemen tengah dengan elemen yang dicari.
- Jika cocok, kembalikan indeksnya.
- Jika elemen yang dicari lebih kecil dari elemen tengah, periksa bagian kiri.
- Jika elemen yang dicari lebih besar, periksa bagian kanan.
- Ulangi hingga elemen ditemukan atau indeks awal lebih besar dari indeks akhir.
Analisis Best Case – Worst Case pada Algoritma Pencarian Biner
✅ Best Case:
Kondisi terbaik saat pencarian dilakukan, dimana data ditemukan dengan cepat:
- Data berada tepat di tengah daftar terurut pada pencarian pertama.
- Data ditemukan dengan cepat dalam daftar kecil yang sudah diurutkan (misalnya 8 atau 16 data).
- Jumlah data cukup banyak tetapi posisi data sangat dekat dengan titik tengah.
❌ Worst Case:
Kondisi terburuk saat pencarian dilakukan, dimana pencarian memakan waktu paling lama:
- Data tidak ada dalam daftar yang sangat besar (misalnya 1.000 atau 10.000 data), sehingga proses pembagian dua dilakukan terus-menerus.
- Data berada di ujung kiri atau kanan, memerlukan beberapa kali pembagian untuk mencapainya.
- Daftar sangat besar, dan data berada jauh dari tengah, sehingga pencarian berlangsung cukup lama meskipun tetap efisien.

Perhatikan barisan angka berikut ini:
Dari barisan angka di atas, berapa langkah yang dibutuhkan untuk menemukan angka 16 dengan algoritma pencarian biner?
Perhatikan barisan angka berikut ini:
Dari barisan angka di atas, berapa langkah yang dibutuhkan untuk menemukan angka 15 dengan algoritma pencarian biner?
Perhatikan barisan angka berikut ini:
Dari barisan angka di atas, berapa langkah yang dibutuhkan untuk menemukan angka 12 dengan algoritma pencarian biner?
Perhatikan barisan angka berikut ini:
Dari barisan angka di atas, berapa langkah yang dibutuhkan untuk menemukan angka 10 dengan algoritma pencarian biner?
Perhatikan barisan angka berikut ini:
Dari barisan angka di atas, berapa langkah yang dibutuhkan untuk menemukan angka 1 dengan algoritma pencarian biner?
Perhatikan barisan angka berikut ini:
Dari barisan angka di atas, berapa langkah yang dibutuhkan untuk menemukan angka 800 dengan algoritma pencarian biner?
Perhatikan barisan angka berikut ini:
Dari barisan angka di atas, berapa langkah yang dibutuhkan untuk menemukan angka 28 dengan algoritma pencarian biner?